「数理演算の基礎」

2019年より着手した「数理再勉強」用の倉庫。

【ユークリッド距離】円関数（Circle function）概念の歴史的限界について。

一般に「三平方の定理（Three square theorem）」あるいは「ピタゴラスの定理（Pythagorean theorem）」として知られるX^2+Y^2=Z^2の式、すなわち単位円（Unit Circle、半径1の円弧）上ではx^2+y^2=1、 単位球面（Unit Circle、半径1の円弧）上ではx^2+y^2+z^2=1、となる定理について。しばしばYの値をXで求める関数に変換されたY=sqrt(1-X^2)の形式でも用いられます。

f:id:ochimusha01:20191029192220g:plain

しかしこの定理は実は数学史上、ある段階まで「半円しか描けない」「従ってY=sqrt(1-X^2)の式とY=-sqrt(1-X^2)の式のセットで運用するもの」と考えられていたのです。

f:id:ochimusha01:20200307040446g:plain

 

統計言語Rによるプログラミング例

#CFS=Circle Function Single
CFS<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2)")

#塗りつぶし（背景）
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（三角）
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色
#線追加（三角）
segments(cx[Radian],cy[Radian],cx[Radian],0,col=c(100,100,100))

#文字追加
text(c(-1,cx[Radian],1,cx[Radian]),c(0,cy[Radian],0,0), labels=c("a","b","c","d"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2))

}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
　CFS(i)
}
}, interval = 0.1, movie.name = "CFS02.gif")

  • xの値が1から0を経て-1にかけて遷移する関数y=sqrt(1-x^2)の内容は三角関数(Trigonometric function)的に表現(expression)すると、角度θの0ラジアン(0度)からπ/2ラジアン(90度)を経てπラジアン(180度)に向かう変遷を扱った形となる。頂点bおよび頂点dのx値がCos(θ),頂点bのy値がSin(θ)に対応。

f:id:ochimusha01:20200307061551g:plain

統計言語Rによるプログラミング例

#CFD=Circle Function Double
CFD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2) &-sqrt(1-X^2) ")

par(new=T)#上書き指定

plot(cx,-1*cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")

#塗りつぶし（上背景）
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色
#塗りつぶし（下背景）

polygon(cx, #x
-cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（上三角）
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#塗りつぶし（下三角）
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(1,cx1[Radian],-1), #x
c(0,cy1[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#線追加（三角）

segments(cx[Radian],cy[Radian],cx[Radian],0,col=rgb(0,0,1))
segments(cx1[Radian],cy1[Radian],cx1[Radian],0,col=rgb(1,0,0))
#文字追加
text(c(-1,cx[Radian],1,cx[Radian],-cx[Radian],-cx[Radian]),c(0,cy[Radian],0,0,-cy[Radian],0), labels=c("a","b","c","d","e","f"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2,2))
#凡例
legend("bottomright", legend=c("sqrt(1-X^2)","-sqrt(1-X^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0))) 

}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
　CFD(i)
}
}, interval = 0.1, movie.name = "CFD03.gif")

  • xの値が-1から0を経て1にかけて遷移する関数y=-sqrt(1-x^2)の内容は三角関数(Trigonometric function)的に表現(expression)すると、角度θのπラジアン(180度)から3/4πラジアン(270度)あるいは-πラジアン(~90度)を経て0ラジアン(0度)に向かう変遷を扱った形となる。頂点eおよび頂点fのx値が-Cos(θ),頂点eのy値が-Sin(θ)に対応。

「半円しか描けない」は、正確には以下の状態を指します。

  • Xの関数としてYを求める場合には（0除算が発生しない）第一象限（X=>0かつY=>0）と第二象限（X=<0かつY=>0）の場合のみ有効。
  • Yの関数としてXを求める場合には（0除算が発生しない）第一象限（X=>0かつY=>0）と第四象限（Y=<0かつX=>0）の場合み有効。

f:id:ochimusha01:20200307062629g:plain
統計言語Rによるプログラミング例

#CFS90Sift=Circle Function Single 90Sift
CFS90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",main="X^2+Y^2=1",xlab="sqrt(1-Y^2)",ylab="Y")

#塗りつぶし（背景）
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（三角）
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色
#線追加（三角）
segments(cy[Radian],cx[Radian],0,cx[Radian],col=c(100,100,100))

#文字追加
text(c(0,cy[Radian],0,0),c(1,cx[Radian],-1,cx[Radian]), labels=c("a","b","c","d"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2))

}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
　CFS90Sift(i)
}
}, interval = 0.1, movie.name = "CFS90Sift01.gif")

  • yの値が1から0を経て-1にかけて遷移する関数x=sqrt(1-y^2)の内容は三角関数(Trigonometric function)的に表現(expression)すると、角度θのπ/2ラジアン(90度)から0ラジアン(0度)を経て3/4πラジアン(270度)あるいは-πラジアン(~90度)に向かう変遷を扱った形となる。頂点bのx値がCos(θ),頂点bおよび頂点dのy値がSin(θ)に対応。

f:id:ochimusha01:20200307065344g:plain

統計言語Rによるプログラミング例

#CFD90Sift=Circle Function Double 90Sift
CFD90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2) &-sqrt(1-Y^2)",ylab="Y")

par(new=T)#上書き指定

plot(cy*-1,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")

#塗りつぶし（上背景）
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色
#塗りつぶし（下背景）

polygon(-cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（上三角）
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#塗りつぶし（下三角）
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(0,cy1[Radian],0), #x
c(1,cx1[Radian],-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#線追加（三角）
segments(cy[Radian],cx[Radian],0,cx[Radian],col=rgb(0,0,1))
segments(cy1[Radian],cx1[Radian],0,cx1[Radian],col=rgb(1,0,0))

#文字追加
text(c(0,cy[Radian],0,0,-cy[Radian],0),c(1,cx[Radian],-1,cx[Radian],-cx[Radian],-cx[Radian]), labels=c("a","b","c","d","e","f"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2,2))
#凡例
legend("bottomright", legend=c("sqrt(1-Y^2)","-sqrt(1-Y^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0))) 

}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
　CFD90Sift(i)
}
}, interval = 0.1, movie.name = "CFD90Sift02.gif")

  • yの値が-1から0を経て1にかけて遷移する関数x=-sqrt(1-y^2)の内容は三角関数(Trigonometric function)的に表現(expression)すると、角度θのπ/2ラジアン(90度)からπラジアン(180度)を経て3/4πラジアン(270度)あるいは-πラジアン(~90度)に向かう変遷を扱った形となる。頂点eおよび頂点fのx値が-Cos(θ),頂点eのy値が-Sin(θ)に対応。

 

 

ちなみに…

  • 角adbと角cdbが直角、すなわちπ/2ラジアン(90度)に保たれ続けるので、三角形の内角の和がπラジアン(180度)となる性質から（その残りである）角dbc=角dab(角度θに従い0ラジアン(0度)からπラジアン(180度)にかけて変遷)と角bcd=角dab(角度-θに従いπラジアン(180度)から0ラジアン(0度)にかけて遷移)の和もまた直角に保たれ続ける。半径Rの円に内接する三角形ABCにおける正弦定理（law of sines）線分AB/Sin(角BCA)=線分BC/Sin(角CAB)=線分CA/Sin(角ABC)=2πRの特殊例。

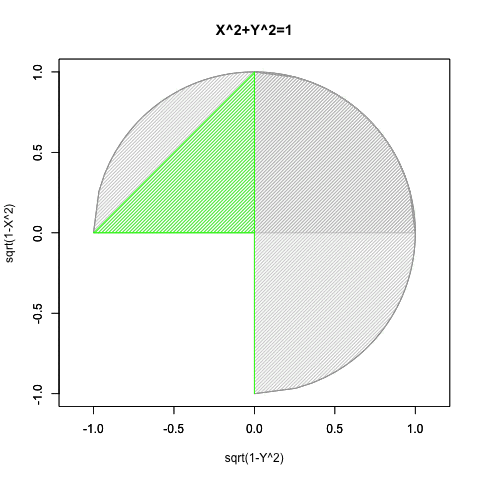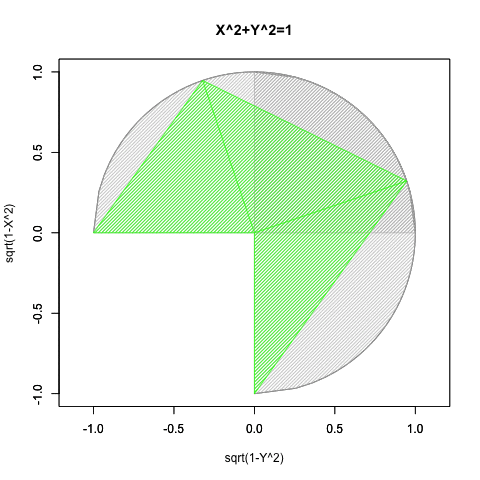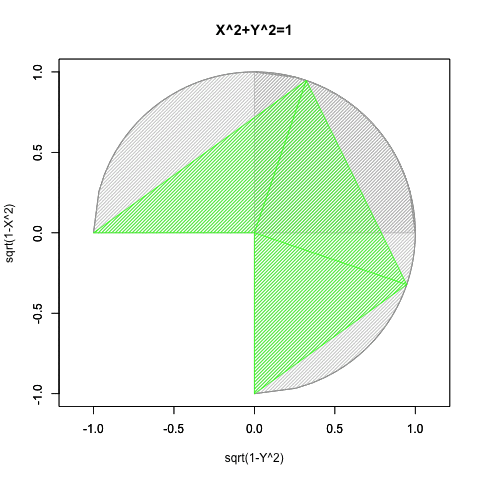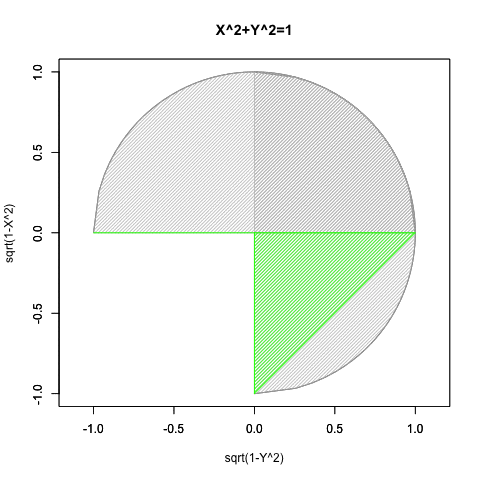
要するにこのアプローチによっては手が出せないのは、第三象限（X=<0かつY=<0）のみという事になるのです。

f:id:ochimusha01:20200307074139g:plain
統計言語Rによるプログラミング例

#CFC=Circle Function Closs
CFC<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2)",ylab="sqrt(1-X^2)")

par(new=T)#上書き指定

plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")

#塗りつぶし（X軸）
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（Y軸）
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（三角）
cx1<-rev(cx)
cy1<-rev(cy)
polygon(c(-1,cx[Radian],cy1[Radian],0,0,-1), #x
c(0,cy[Radian],cx1[Radian],-1,0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#線追加（三角）
segments(cx[Radian],cy[Radian],0,0,col=rgb(0,1,0))
segments(cy1[Radian],cx1[Radian],0,0,col=rgb(0,1,0))

#文字追加
text(c(-1,cx[Radian],cy1[Radian],0,0),c(0,cy[Radian],cx1[Radian],-1,0), labels=c("a","b","c","d","e"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2))

}
#アニメーション
library("animation")
Time_Code=rev(c(1:60))
saveGIF({
for (i in Time_Code){
　CFC(i)
}
}, interval = 0.1, movie.name = "CFC01.gif")

以下続報…