【ユークリッド距離】物理学における等速円運動解析(Constant velocity circular motion)概念の登場
以下の様に数学方面からの円描画方法の探索は歴史的に行き詰ってしまった訳ですが…



ある意味かかる閉塞状態を打破したのが物理学における等速円運動解析(Constant velocity circular motion)概念の登場だったとも考えられる訳です。
回転運動を回転面上の観測者が真横から見ると物体は単振動しているように見える。あるいは、物体のx座標とy座標は互いに位相が90度=π/2ずれた単振動を行っている。
振動運動では回転速度のことを周波数または振動数と呼ぶ。
①まず「あらゆる運動の原型の一つ」たる等速円運動(Constant Velocity Circular Motion)を想定する。

統計言語Rによる作図例
#CVCM=等速円運動(Constant Velocity Circular Motion)
#Radian=角度(60分割)
CVCM<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),main="Constant Velocity Circular Motion",xlab="cos(θ)",ylab="sin(θ)")#塗りつぶし(円)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))segments(cx[Radian],cy[Radian],0,0,col=rgb(1,0,0))
#凡例
legend("bottomright", legend=c("side=2π/1τ","radius=1"), lty=c(1,1), col=c(rgb(0,1,0),rgb(1,0,0)))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CVCM(i)
}
}, interval = 0.1, movie.name = "CVCM01.gif")
②回転運動を互いに直交するX軸側とY軸側から観測すると、同じ波形が互いに位相が90度=π/2ずれた単振動が得られる(Cos波とSin波)逆にこの組み合わせによって回転運動を説明する事も出来る。
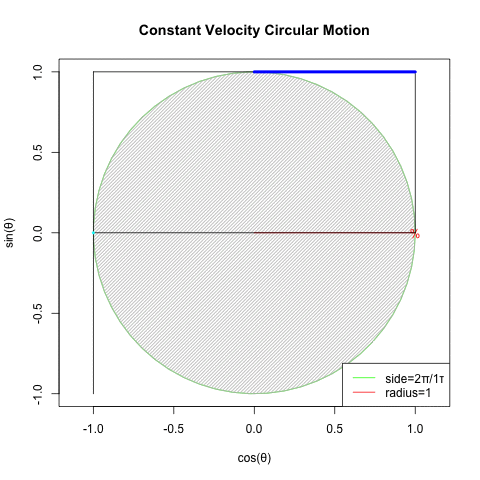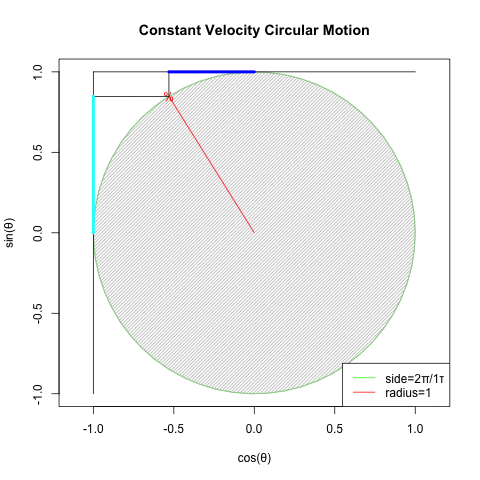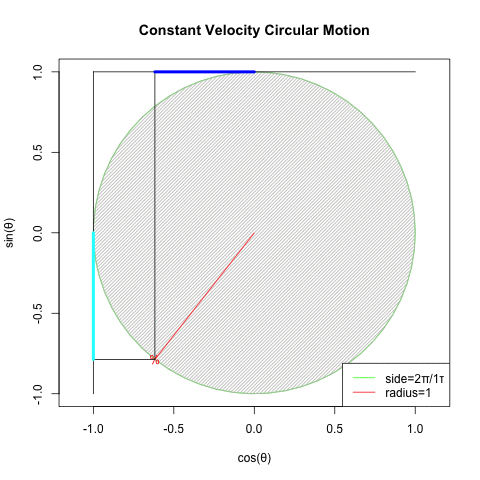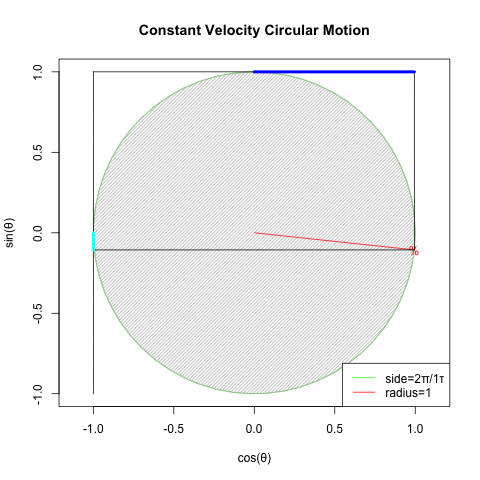
XY軸(円弧)
#CosSin=Cos波とSin波の検出
#Radian=角度(60分割)
CosSin<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),main="Constant Velocity Circular Motion",xlab="cos(θ)",ylab="sin(θ)")#塗りつぶし(円)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))#補助線
segments(cx[Radian],cy[Radian],0,0,col=rgb(1,0,0))
#Cos
segments(-1,1,1,1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],cx[Radian],1,col=rgb(0,0,0))
segments(0,1,cx[Radian],1,col=rgb(0,0,1),lwd =4)
#Sin
segments(-1,1,-1,-1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],-1,cy[Radian],col=rgb(0,0,0))
segments(-1,0,-1,cy[Radian],col=rgb(0,1,1),lwd =4)
#凡例
legend("bottomright", legend=c("side=2π/1τ","radius=1"), lty=c(1,1), col=c(rgb(0,1,0),rgb(1,0,0)))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CosSin(i)
}
}, interval = 0.1, movie.name = "CosSin01.gif")
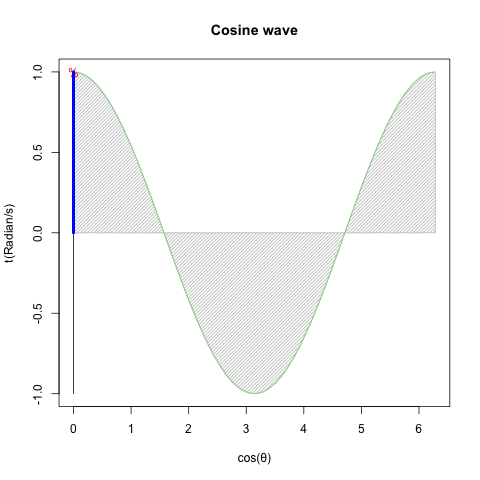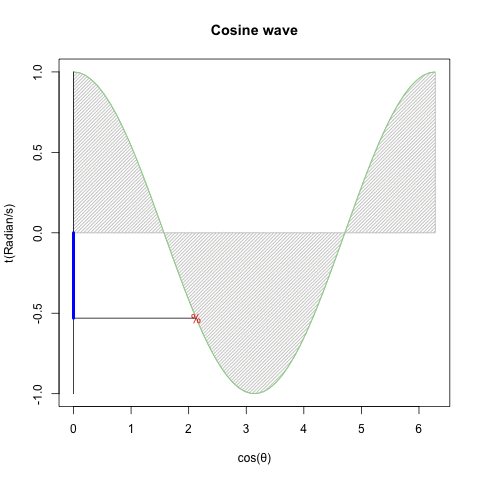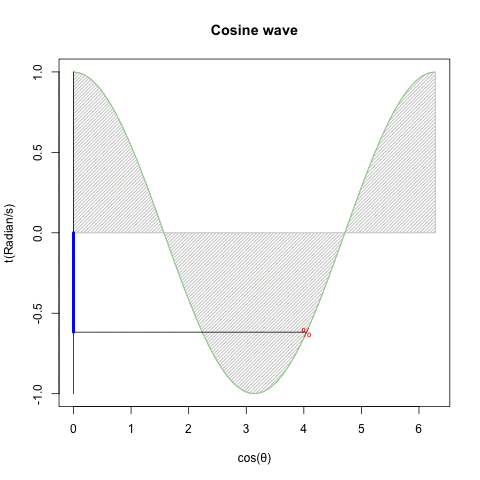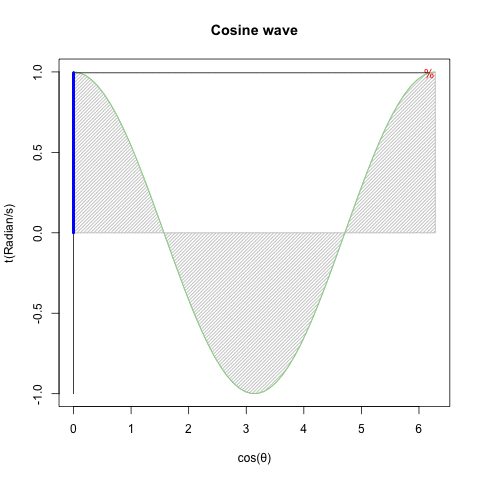
XZ軸(Cos波)
CosCos<-function(Radian){
cx<-seq(0,2*pi,length=60)
cy<-cos(c0)
plot(cx,cy,type="l",col=rgb(0,1,0),ylim=c(-1,1),main="Cosine wave",xlab="cos(θ)",ylab="t(Radian/s)")#塗りつぶし(Cos波)
polygon(c(0,cx,2*pi), #x
c(0,cy,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))#補助線
segments(0,-1,0,1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],0,cy[Radian],col=rgb(0,0,0))
segments(0,0,0,cy[Radian],col=rgb(0,0,1),lwd =4)
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CosCos(i)
}
}, interval = 0.1, movie.name = "CosCos01.gif")

YZ軸(Sin波)
SinSin<-function(Radian){
cx<-seq(0,2*pi,length=60)
cy<-sin(c0)
plot(cx,cy,type="l",col=rgb(0,1,0),ylim=c(-1,1),main="Sine wave",xlab="cos(θ)",ylab="t(Radian/s)")#塗りつぶし(Cos波)
polygon(c(0,cx,2*pi), #x
c(0,cy,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))
#補助線
segments(0,-1,0,1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],0,cy[Radian],col=rgb(0,0,0))
segments(0,0,0,cy[Radian],col=rgb(0,1,1),lwd =4)
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
SinSin(i)
}
}, interval = 0.1, movie.name = "SinSin01.gif")
③ちなみにこのアプローチにおいては(数学における)角度θの概念が角速度(Angular velocity、単位Radian/S)または周波数(frequency、単位Hz)として検出されるので、最終的に構成されるのも「(空間概念としてのみ意識される)単位円(Unit Circle、半径1)」ではなく「(空間として認識されるZ軸と時間経過として意識されるt軸の存在も考えた)単位円筒(Unit Cylinder、半径1、周期1)」となる。

XY軸(円弧)

ZX軸(Cos波)

ZY軸(Sin波)

統計言語Rによる描画例
library(rgl)
Rtime<-seq(0,2*pi,length=60)
CosX<-cos(Rtime)
SinY<-sin(Rtime)
plot3d(CosX,SinY,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2*pi))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01")
統計言語Rによる2Dヒストグラム表示
データ生成
z_axis<-seq(1,-1,length=60)
radian_axis<-seq(0,2*pi,length=60)
x_axis<-cos(radian_axis)
y_axis<-sin(radian_axis)
polygon_60 <- data.frame(X=x_axis, Y=y_axis,Z=z_axis)
library(xtable)
print(xtable(round(polygon_60, digits = 6)), type = "html")
| X | Y | Z | |
|---|---|---|---|
| 1 | 1.00 | 0.00 | 1.00 |
| 2 | 0.99 | 0.11 | 0.97 |
| 3 | 0.98 | 0.21 | 0.93 |
| 4 | 0.95 | 0.31 | 0.90 |
| 5 | 0.91 | 0.41 | 0.86 |
| 6 | 0.86 | 0.51 | 0.83 |
| 7 | 0.80 | 0.60 | 0.80 |
| 8 | 0.73 | 0.68 | 0.76 |
| 9 | 0.66 | 0.75 | 0.73 |
| 10 | 0.57 | 0.82 | 0.69 |
| 11 | 0.48 | 0.87 | 0.66 |
| 12 | 0.39 | 0.92 | 0.63 |
| 13 | 0.29 | 0.96 | 0.59 |
| 14 | 0.19 | 0.98 | 0.56 |
| 15 | 0.08 | 1.00 | 0.53 |
| 16 | -0.03 | 1.00 | 0.49 |
| 17 | -0.13 | 0.99 | 0.46 |
| 18 | -0.24 | 0.97 | 0.42 |
| 19 | -0.34 | 0.94 | 0.39 |
| 20 | -0.44 | 0.90 | 0.36 |
| 21 | -0.53 | 0.85 | 0.32 |
| 22 | -0.62 | 0.79 | 0.29 |
| 23 | -0.70 | 0.72 | 0.25 |
| 24 | -0.77 | 0.64 | 0.22 |
| 25 | -0.83 | 0.55 | 0.19 |
| 26 | -0.89 | 0.46 | 0.15 |
| 27 | -0.93 | 0.36 | 0.12 |
| 28 | -0.96 | 0.26 | 0.08 |
| 29 | -0.99 | 0.16 | 0.05 |
| 30 | -1.00 | 0.05 | 0.02 |
| 31 | -1.00 | -0.05 | -0.02 |
| 32 | -0.99 | -0.16 | -0.05 |
| 33 | -0.96 | -0.26 | -0.08 |
| 34 | -0.93 | -0.36 | -0.12 |
| 35 | -0.89 | -0.46 | -0.15 |
| 36 | -0.83 | -0.55 | -0.19 |
| 37 | -0.77 | -0.64 | -0.22 |
| 38 | -0.70 | -0.72 | -0.25 |
| 39 | -0.62 | -0.79 | -0.29 |
| 40 | -0.53 | -0.85 | -0.32 |
| 41 | -0.44 | -0.90 | -0.36 |
| 42 | -0.34 | -0.94 | -0.39 |
| 43 | -0.24 | -0.97 | -0.42 |
| 44 | -0.13 | -0.99 | -0.46 |
| 45 | -0.03 | -1.00 | -0.49 |
| 46 | 0.08 | -1.00 | -0.53 |
| 47 | 0.19 | -0.98 | -0.56 |
| 48 | 0.29 | -0.96 | -0.59 |
| 49 | 0.39 | -0.92 | -0.63 |
| 50 | 0.48 | -0.87 | -0.66 |
| 51 | 0.57 | -0.82 | -0.69 |
| 52 | 0.66 | -0.75 | -0.73 |
| 53 | 0.73 | -0.68 | -0.76 |
| 54 | 0.80 | -0.60 | -0.80 |
| 55 | 0.86 | -0.51 | -0.83 |
| 56 | 0.91 | -0.41 | -0.86 |
| 57 | 0.95 | -0.31 | -0.90 |
| 58 | 0.98 | -0.21 | -0.93 |
| 59 | 0.99 | -0.11 | -0.97 |
| 60 | 1.00 | -0.00 | -1.00 |
二次元空間に円(60角形)を描く。
plot(polygon_60$X,polygon_60$Y,asp=1,type="l",main="Regular Polygon 60",xlab="X",ylab="Y")

三次元空間に円周(60角形)を描く。
library(rgl)
plot3d(polygon_60$X,polygon_60$Y,polygon_60$Z,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),,main="Regular Polygon 60",xlab="X",ylab="Y",zlab="Z")
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01A")


X軸-Y軸
*要するに均等な間隔で円弧を描いている。
library(gplots)
polygon_60_hist2d<-function(x){
# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(polygon_60$X, polygon_60$Y, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="polygon 60 with hist2d()",xlab="x",ylab="y",zlab="counts")}
#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
polygon_60_hist2d(i)
}
}, interval = 0.1, movie.name = "polygon_60_hist2d.gif")

X軸-Z軸
*要するに均等な間隔でCos波を描いている。
library(gplots)
polygon_60_hist2d<-function(x){
# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(polygon_60$X, polygon_60$Z, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="polygon 60 with hist2d()",xlab="x",ylab="z",zlab="counts")}
#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
polygon_60_hist2d(i)
}
}, interval = 0.1, movie.name = "polygon_60_hist2d.gif")

Y軸-Z軸
*要するに均等な間隔でSin波を描いている。
library(gplots)
polygon_60_hist2d<-function(x){
# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(polygon_60$Y, polygon_60$Z, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="polygon 60 with hist2d()",xlab="y",ylab="z",zlab="counts")}
#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
polygon_60_hist2d(i)
}
}, interval = 0.1, movie.name = "polygon_60_hist2d.gif")

ここで興味深いのが一般に「三平方の定理(Three square theorem)」あるいは「ピタゴラスの定理(Pythagorean theorem)」として知られるX^2+Y^2=Z^2の式、すなわち単位円(Unit Circle、半径1の円弧)上ではx^2+y^2=1、 単位球面(Unit Circle、半径1の円弧)上ではx^2+y^2+z^2=1、となる定理との関係。しばしばYの値をXで求める関数に変換されたY=sqrt(1-X^2)の形式でも用いられる訳ですが…
- コンピューター言語は無限大Infの辺数と無限小-Infの辺長で構成される円そのもの(circle itself)を直接は扱えないので、これを適切な精度が得られる正多角形として扱うしかない(このサイトでは主に正60角形を採用)。
- その状態で上掲式を適用するとヒストグラムとしてNoD(Number of Divide=分割数)に対応する半径長の線分集合が得られるのである。
統計言語Rによる実装例
#円データ自体は上掲プログラムからの流用
Radius_60<-data.frame(Radius=polygon_60$X^2+polygon_60$Y^2)
print(xtable(round(Radius_60, digits = 6)), type = "html")
| Radius | |
|---|---|
| 1 | 1.00 |
| 2 | 1.00 |
| 3 | 1.00 |
| 4 | 1.00 |
| 5 | 1.00 |
| 6 | 1.00 |
| 7 | 1.00 |
| 8 | 1.00 |
| 9 | 1.00 |
| 10 | 1.00 |
| 11 | 1.00 |
| 12 | 1.00 |
| 13 | 1.00 |
| 14 | 1.00 |
| 15 | 1.00 |
| 16 | 1.00 |
| 17 | 1.00 |
| 18 | 1.00 |
| 19 | 1.00 |
| 20 | 1.00 |
| 21 | 1.00 |
| 22 | 1.00 |
| 23 | 1.00 |
| 24 | 1.00 |
| 25 | 1.00 |
| 26 | 1.00 |
| 27 | 1.00 |
| 28 | 1.00 |
| 29 | 1.00 |
| 30 | 1.00 |
| 31 | 1.00 |
| 32 | 1.00 |
| 33 | 1.00 |
| 34 | 1.00 |
| 35 | 1.00 |
| 36 | 1.00 |
| 37 | 1.00 |
| 38 | 1.00 |
| 39 | 1.00 |
| 40 | 1.00 |
| 41 | 1.00 |
| 42 | 1.00 |
| 43 | 1.00 |
| 44 | 1.00 |
| 45 | 1.00 |
| 46 | 1.00 |
| 47 | 1.00 |
| 48 | 1.00 |
| 49 | 1.00 |
| 50 | 1.00 |
| 51 | 1.00 |
| 52 | 1.00 |
| 53 | 1.00 |
| 54 | 1.00 |
| 55 | 1.00 |
| 56 | 1.00 |
| 57 | 1.00 |
| 58 | 1.00 |
| 59 | 1.00 |
| 60 | 1.00 |
データ諸元
#最大値
max(Radius_60$Radius)
[1] 1
#最小値
min(Radius_60$Radius)
[1] 1
#中央値
median(Radius_60$Radius)
[1] 1
最頻値
hr <- hist(Radius_60$Radius,,col=rgb(1,0,0))
n <- length(hr$counts) # 階級の数
class_names <- NULL # 階級の名前格納用
for(i in 1:n) {
class_names[i] <- paste(hr$breaks[i], "~", hr$breaks[i+1])
}
hr_table <- data.frame(class=class_names, frequency=hr$counts)library(xtable)
print(xtable(hr_table), type = "html")

| class | frequency | |
|---|---|---|
| 1 | 0 ~ 1 | 60 |
偏差追加
#平均(mean)
Radius_60_mean<-mean(Radius_60$Radius)
Radius_60_mean
[1] 1#偏差(Deviation)
Radius_60$Deviation<-Radius_60$Radius-Radius_60_mean
library(xtable)
print(xtable(Radius_60), type = "html")
| Radius | Deviation | |
|---|---|---|
| 1 | 1.00 | 0.00 |
| 2 | 1.00 | -0.00 |
| 3 | 1.00 | 0.00 |
| 4 | 1.00 | -0.00 |
| 5 | 1.00 | 0.00 |
| 6 | 1.00 | -0.00 |
| 7 | 1.00 | -0.00 |
| 8 | 1.00 | 0.00 |
| 9 | 1.00 | 0.00 |
| 10 | 1.00 | 0.00 |
| 11 | 1.00 | -0.00 |
| 12 | 1.00 | 0.00 |
| 13 | 1.00 | 0.00 |
| 14 | 1.00 | -0.00 |
| 15 | 1.00 | 0.00 |
| 16 | 1.00 | 0.00 |
| 17 | 1.00 | 0.00 |
| 18 | 1.00 | -0.00 |
| 19 | 1.00 | 0.00 |
| 20 | 1.00 | 0.00 |
| 21 | 1.00 | 0.00 |
| 22 | 1.00 | 0.00 |
| 23 | 1.00 | 0.00 |
| 24 | 1.00 | 0.00 |
| 25 | 1.00 | 0.00 |
| 26 | 1.00 | 0.00 |
| 27 | 1.00 | 0.00 |
| 28 | 1.00 | 0.00 |
| 29 | 1.00 | 0.00 |
| 30 | 1.00 | 0.00 |
| 31 | 1.00 | 0.00 |
| 32 | 1.00 | -0.00 |
| 33 | 1.00 | 0.00 |
| 34 | 1.00 | 0.00 |
| 35 | 1.00 | 0.00 |
| 36 | 1.00 | 0.00 |
| 37 | 1.00 | -0.00 |
| 38 | 1.00 | 0.00 |
| 39 | 1.00 | -0.00 |
| 40 | 1.00 | -0.00 |
| 41 | 1.00 | 0.00 |
| 42 | 1.00 | 0.00 |
| 43 | 1.00 | -0.00 |
| 44 | 1.00 | -0.00 |
| 45 | 1.00 | -0.00 |
| 46 | 1.00 | 0.00 |
| 47 | 1.00 | 0.00 |
| 48 | 1.00 | 0.00 |
| 49 | 1.00 | 0.00 |
| 50 | 1.00 | 0.00 |
| 51 | 1.00 | 0.00 |
| 52 | 1.00 | 0.00 |
| 53 | 1.00 | 0.00 |
| 54 | 1.00 | 0.00 |
| 55 | 1.00 | -0.00 |
| 56 | 1.00 | 0.00 |
| 57 | 1.00 | 0.00 |
| 58 | 1.00 | -0.00 |
| 59 | 1.00 | 0.00 |
| 60 | 1.00 | 0.00 |
Z得点追加
#分散
Radius_60_Dispersion<-sum*1^2)/length(Radius_60$Radius)
Radius_60_Dispersion
[1] 0
#標準偏差
Radius_60_Standard_Dispersion<-sqrt(Radius_60_Dispersion)
Radius_60_Standard_Dispersion
[1] 0#Z得点(平均値1,標準偏差1)偏差/標準偏差
Radius_60$Zvalue<-Radius_60$Deviation/Radius_60_Standard_Dispersion
print(xtable(Radius_60), type = "html")
*実際には0除算が発生して計算不可能
| Radius | Deviation | Zvalue | |
|---|---|---|---|
| 1 | 1.00 | 0.00 | 0.00 |
| 2 | 1.00 | -0.00 | -0.00 |
| 3 | 1.00 | 0.00 | 0.00 |
| 4 | 1.00 | -0.00 | -0.00 |
| 5 | 1.00 | 0.00 | 0.00 |
| 6 | 1.00 | -0.00 | -0.00 |
| 7 | 1.00 | -0.00 | -0.00 |
| 8 | 1.00 | 0.00 | 0.00 |
| 9 | 1.00 | 0.00 | 0.00 |
| 10 | 1.00 | 0.00 | 0.00 |
| 11 | 1.00 | -0.00 | -0.00 |
| 12 | 1.00 | 0.00 | 0.00 |
| 13 | 1.00 | 0.00 | 0.00 |
| 14 | 1.00 | -0.00 | -0.00 |
| 15 | 1.00 | 0.00 | 0.00 |
| 16 | 1.00 | 0.00 | 0.00 |
| 17 | 1.00 | 0.00 | 0.00 |
| 18 | 1.00 | -0.00 | -0.00 |
| 19 | 1.00 | 0.00 | 0.00 |
| 20 | 1.00 | 0.00 | 0.00 |
| 21 | 1.00 | 0.00 | 0.00 |
| 22 | 1.00 | 0.00 | 0.00 |
| 23 | 1.00 | 0.00 | 0.00 |
| 24 | 1.00 | 0.00 | 0.00 |
| 25 | 1.00 | 0.00 | 0.00 |
| 26 | 1.00 | 0.00 | 0.00 |
| 27 | 1.00 | 0.00 | 0.00 |
| 28 | 1.00 | 0.00 | 0.00 |
| 29 | 1.00 | 0.00 | 0.00 |
| 30 | 1.00 | 0.00 | 0.00 |
| 31 | 1.00 | 0.00 | 0.00 |
| 32 | 1.00 | -0.00 | -0.00 |
| 33 | 1.00 | 0.00 | 0.00 |
| 34 | 1.00 | 0.00 | 0.00 |
| 35 | 1.00 | 0.00 | 0.00 |
| 36 | 1.00 | 0.00 | 0.00 |
| 37 | 1.00 | -0.00 | -0.00 |
| 38 | 1.00 | 0.00 | 0.00 |
| 39 | 1.00 | -0.00 | -0.00 |
| 40 | 1.00 | -0.00 | -0.00 |
| 41 | 1.00 | 0.00 | 0.00 |
| 42 | 1.00 | 0.00 | 0.00 |
| 43 | 1.00 | -0.00 | -0.00 |
| 44 | 1.00 | -0.00 | -0.00 |
| 45 | 1.00 | -0.00 | -0.00 |
| 46 | 1.00 | 0.00 | 0.00 |
| 47 | 1.00 | 0.00 | 0.00 |
| 48 | 1.00 | 0.00 | 0.00 |
| 49 | 1.00 | 0.00 | 0.00 |
| 50 | 1.00 | 0.00 | 0.00 |
| 51 | 1.00 | 0.00 | 0.00 |
| 52 | 1.00 | 0.00 | 0.00 |
| 53 | 1.00 | 0.00 | 0.00 |
| 54 | 1.00 | 0.00 | 0.00 |
| 55 | 1.00 | -0.00 | -0.00 |
| 56 | 1.00 | 0.00 | 0.00 |
| 57 | 1.00 | 0.00 | 0.00 |
| 58 | 1.00 | -0.00 | -0.00 |
| 59 | 1.00 | 0.00 | 0.00 |
| 60 | 1.00 | 0.00 | 0.00 |
偏差値追加
Radius_60$Deviation_value<-Radius_60$Zvalue*10+50
library(xtable)
print(xtable(Radius_60), type = "html")
| Radius | Deviation | Zvalue | Deviation_value | |
|---|---|---|---|---|
| 1 | 1.00 | 0.00 | 0.00 | 50.00 |
| 2 | 1.00 | -0.00 | -0.00 | 50.00 |
| 3 | 1.00 | 0.00 | 0.00 | 50.00 |
| 4 | 1.00 | -0.00 | -0.00 | 50.00 |
| 5 | 1.00 | 0.00 | 0.00 | 50.00 |
| 6 | 1.00 | -0.00 | -0.00 | 50.00 |
| 7 | 1.00 | -0.00 | -0.00 | 50.00 |
| 8 | 1.00 | 0.00 | 0.00 | 50.00 |
| 9 | 1.00 | 0.00 | 0.00 | 50.00 |
| 10 | 1.00 | 0.00 | 0.00 | 50.00 |
| 11 | 1.00 | -0.00 | -0.00 | 50.00 |
| 12 | 1.00 | 0.00 | 0.00 | 50.00 |
| 13 | 1.00 | 0.00 | 0.00 | 50.00 |
| 14 | 1.00 | -0.00 | -0.00 | 50.00 |
| 15 | 1.00 | 0.00 | 0.00 | 50.00 |
| 16 | 1.00 | 0.00 | 0.00 | 50.00 |
| 17 | 1.00 | 0.00 | 0.00 | 50.00 |
| 18 | 1.00 | -0.00 | -0.00 | 50.00 |
| 19 | 1.00 | 0.00 | 0.00 | 50.00 |
| 20 | 1.00 | 0.00 | 0.00 | 50.00 |
| 21 | 1.00 | 0.00 | 0.00 | 50.00 |
| 22 | 1.00 | 0.00 | 0.00 | 50.00 |
| 23 | 1.00 | 0.00 | 0.00 | 50.00 |
| 24 | 1.00 | 0.00 | 0.00 | 50.00 |
| 25 | 1.00 | 0.00 | 0.00 | 50.00 |
| 26 | 1.00 | 0.00 | 0.00 | 50.00 |
| 27 | 1.00 | 0.00 | 0.00 | 50.00 |
| 28 | 1.00 | 0.00 | 0.00 | 50.00 |
| 29 | 1.00 | 0.00 | 0.00 | 50.00 |
| 30 | 1.00 | 0.00 | 0.00 | 50.00 |
| 31 | 1.00 | 0.00 | 0.00 | 50.00 |
| 32 | 1.00 | -0.00 | -0.00 | 50.00 |
| 33 | 1.00 | 0.00 | 0.00 | 50.00 |
| 34 | 1.00 | 0.00 | 0.00 | 50.00 |
| 35 | 1.00 | 0.00 | 0.00 | 50.00 |
| 36 | 1.00 | 0.00 | 0.00 | 50.00 |
| 37 | 1.00 | -0.00 | -0.00 | 50.00 |
| 38 | 1.00 | 0.00 | 0.00 | 50.00 |
| 39 | 1.00 | -0.00 | -0.00 | 50.00 |
| 40 | 1.00 | -0.00 | -0.00 | 50.00 |
| 41 | 1.00 | 0.00 | 0.00 | 50.00 |
| 42 | 1.00 | 0.00 | 0.00 | 50.00 |
| 43 | 1.00 | -0.00 | -0.00 | 50.00 |
| 44 | 1.00 | -0.00 | -0.00 | 50.00 |
| 45 | 1.00 | -0.00 | -0.00 | 50.00 |
| 46 | 1.00 | 0.00 | 0.00 | 50.00 |
| 47 | 1.00 | 0.00 | 0.00 | 50.00 |
| 48 | 1.00 | 0.00 | 0.00 | 50.00 |
| 49 | 1.00 | 0.00 | 0.00 | 50.00 |
| 50 | 1.00 | 0.00 | 0.00 | 50.00 |
| 51 | 1.00 | 0.00 | 0.00 | 50.00 |
| 52 | 1.00 | 0.00 | 0.00 | 50.00 |
| 53 | 1.00 | 0.00 | 0.00 | 50.00 |
| 54 | 1.00 | 0.00 | 0.00 | 50.00 |
| 55 | 1.00 | -0.00 | -0.00 | 50.00 |
| 56 | 1.00 | 0.00 | 0.00 | 50.00 |
| 57 | 1.00 | 0.00 | 0.00 | 50.00 |
| 58 | 1.00 | -0.00 | -0.00 | 50.00 |
| 59 | 1.00 | 0.00 | 0.00 | 50.00 |
| 60 | 1.00 | 0.00 | 0.00 | 50.00 |
まぁ「単位円に内接する多角形の各頂点の中心からの距離」は当然全部1だから「平均=最大値=最小値=中央値=最頻値=1,分散=標準偏差=Z得点=0,偏差値全データ50」となるのですね。以下続報…