【数列概念の拡張】「(共役関係を拡張した)対蹠地効果」に至る道。
今回の出発点はこれ。


- 並べる数に制限を加え、例えば自然数(Natural number)あるいは正数(Positive number)のみを並べるならば、これを自然数列集合(group of NATULAL sequence)Nと略称する。メモリ確保上の必然性から0や負数(Negative number)を扱えないプログラミング言語などにおける配列(array)の添字もこれに該当する。
- 整数、有理数、実数、複素数などのほかの数体系を用いる場合も同様に0と負数を数の定義に加えた整数列集合(group of INTEGER sequence)Z、m/n(ただしmは整数、nは自然数)の形式で定義(definition)される分数(fraction)の概念(独Konzept、英仏concept)を加えた有理数列集合(group of RATIONAL sequence)Q、これにさらに有理数の概念では定義不可能な順序数(ordinal number)としての無理数(Irrational number=無比数)の概念を加えた実数列集合(group of REAL sequence)R、さらに例えばi^2=-1やi^2=j^2=k^2=ijk=-1の形式で定義される虚数(imaginary number)の概念を加えた複素数列集合(group of COMPLEX sequence)Cなる略称を用いる。
この様に数列間の関係は、その特徴による分類で集合(set)によっても表し得るのです。
集合(英set, 仏ensemble, 独Menge) - Wikipedia
大雑把に言えば幾つかの「もの」からなる「集まり」である。数学においては集合を構成する個々の「もの」のことを元 (げん、英element=要素) という。
集合論のみならず現代数学全体における最も基本的な概念の一つであり、現代数学のほとんどが集合と写像の言葉で書かれていると言ってよい。
慣例的に、ある種の集合が系 (system) や族 (family) などと呼ばれることもある。実際には、これらの呼び名に本質的な違いはないが細かなニュアンスの違いを含むと考えられている。たとえば、方程式系(「相互に連立する」方程式の集合)、集合族(「一定の規則に基づく」集合の集合)、加法族(「加法的な性質を持つ」集合族)など。
- 自然数列(Natural sequence)は整数列(Integer sequence)の真部分集合(proper subset)として存在する。
- 偶数列(Even sequence)や奇数列(Odd sequence)は自然数列や整数列の真部分集合(proper subset)として存在する。
この様に数列概念が拡大されるにつれ、それに対応する次元概念も拡張されます。
数学の幾何学においては主にn-次元ユークリッド空間上で定義される。
- 一軸の片側無限数列(One-sided infinite sequence)のみが存在する一次元(One dimensional)空間では半直線(Half line)を構成する。直交座標系(rectangular coordinate system//orthogonal coordinate system)では傾き(slope)1、全ての軸で切片(intercept)0で負数(negative number)を範囲(interval)に含まない一次関数(linear function)で表される。
この様に距離(distance)rの概念しかないところに角度(angle)θφの概念を追加したのが極座標系(polar coordinates system)となる。
上掲の様に同心円弧を構成する場合x=r*cos(θ),y=r*sin(θ), 同心球表面を構成する場合x =r*sin(θ)cos(φ), y=r*sin(θ)sin(φ), z=r*cos(θ)の変換式によって直交座標系の座標に対応する。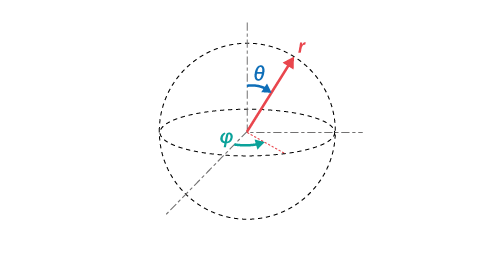
- 2軸の両側無限数列(Two-sided infinite sequence)が直交(Orthogonal)する二次元(One dimensional)空間では、平面4枚に分割された四分儀(Quadrant)を構成する。図の様に一般にはI象限(x軸もY軸も正数)、II象限(X軸は負数、Y軸は正数) III象限(x軸もY軸も負数)、IV象限(X軸は正数、Y軸は負数)と列記されるが、偶数と奇数の振る舞いに重ねる際には00象限(x軸もY軸も正数)、01象限(X軸は負数、Y軸は正数) 02象限(x軸もY軸も負数)、03象限(X軸は正数、Y軸は負数)といった具合にイメージする必要も生じてくる。
- 3軸の両側無限数列が直交する三次元(Three dimensional)空間においては立方体8個に分割された八分儀(Octant)を構成する。I象限/00象限(x軸もY軸もZ軸も正数)、II象限/01象限(X軸は負数、Y軸とZ軸は正数) III象限/02象限(x軸もY軸も負数, Z軸は正数)、IV象限/03象限(X軸は正数、Y軸は負数, Z軸は正数)、V象限/04象限(x軸とY軸は正数、Z軸は負数)、VI象限/05象限(X軸は負数、Y軸は正数、Z軸は負数) VII象限/06象限(x軸もY軸もZ軸も負数)、VIII象限/07象限(X軸は負数、Y軸は正数、Z軸は負数)。
この様にn-次元空間はn本軸の相互直交半空間によって成立し、符号との兼ね合いで2^n個の象限を構成する。
ここで偶数と奇数の連続交代に改めて着目してみましょう。
- 正数を0、負数を1と捉える2進数体系を考える。
- 追加される次元は右手系(right-handed system)または正系(positive- oriented system)の法則に従ってX,Y,Z…と名付けていく。
すると象限は以下の2種類に大別される事になります。
- 全ての桁が0か1の「極象限(Polar orthant)」
- 桁に0と1が混ざった「共益象限(Conjugate orthant)」。
この考え方を具体的に各次元に適用すると以下となります。
- 一次元(x)では極象限0,1に対し共役象限は0個となる。
- 二次元(x,y)では極象限00,11に対し共役象限は01,10の2個となる。
- 三次元(x,y,z)では極象限000,111に対し共役象限は001,010,011,100,101,110の6個となる。
元来「共役」なる概念は「2個でセット」というイメージですが…
ここでは対蹠点効果、すなわち「球表面上のある地点とその対蹠点を結ぶ同距離の経路が無数に存在し得る」概念の受け皿として使っています。実際、3次元空間の球面上で発生するこの効果は、2次元空間の円弧上における共役関係に対応する訳ですから。

統計言語Rによるプログラミング例
#RD=2角形(Regular Digon)
#Radian=角度(60分割)
RD<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",main="Conjugate & antipode effect",xlab="cos(θ)",ylab="sin(θ)")p_max<-15
p0<-seq(pi,0,length=p_max)
px_Hi<-rev(cos(p0))
px_Low<-rev(cos(p0*-1))
py_Hi<-rev(sin(p0))
py_Low<-rev(sin(p0*-1))#左側インジケータ描画(緑)
polygon(c(px_Hi[1:Radian],px_Low[Radian:1]), #x
c(py_Hi[1:Radian],py_Low[Radian:1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
#右側インジケータ描画(赤)
polygon(c(px_Hi[p_max:Radian],px_Low[Radian:p_max]), #x
c(py_Hi[p_max:Radian],py_Low[Radian:p_max]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(1,0,0))#塗りつぶす色
text(x=1,y=0,labels="X",cex=2,col=rgb(0,1,0))
text(x=-1,y=0,labels="X",cex=2,col=rgb(1,0,0))
}
#アニメーション
library("animation")
Time_Code=c(1:15,14:1)
saveGIF({
for (i in Time_Code){
RD(i)
}
}, interval = 0.1, movie.name = "RD01.gif")
考え方
概ね「任意の円弧を2分割する2点(直線距離2に対して円弧上の距離はπ)の円弧上に現れる共役複素数」と「球表面上において出発点「1」とその座標上正反対に位置する対蹠地「−1」の間を(やはり直線距離2に対して球表面上の最短移動距離がπ)無数の測地線」は同一視し得る。
直線の概念を曲がった空間において一般化したものである。測地線の中でその長さが2点間の距離に等しくなるものを最短測地線という。
言葉の由来は、測地学からであり、地球上の2点間の最短ルート(大円の一部)による。この概念は、数学的な空間にも拡張され、例えばグラフ理論ではグラフ上の2つの頂点(vertex)や結節点 (node) 間の測地線が定義されている。一般相対性理論では、光は曲がった空間での測地線を進むという原理に基づいて構築されている。
概要として、単純な例を示す。 地球を単純に球面であるとしよう.地球表面上で生活する我々は,例えば 東京とニューヨークの間を最短距離で移動するためには、東京とニューヨークを通る大円に沿った移動を行えばよく、この大円の一部こそ、測地線と呼ばれるものになる。
しかしながら、一般に、大円をその上の2点で分けると優弧と劣弧に分かれる。東京からニューヨークへ大円に沿った移動をしても、東京からニューヨークに行くには大円の周り方によって遠い移動と近い移動とある。この場合、劣弧に沿って移動すれば最短距離、優弧に沿えば直線的な移動としては最も遠回りになるわけである。大円の一部である弧は測地線となるが、必ずしも2点間の最短距離を示す曲線とはならない。
逆に2点間の最短距離を示す曲線は測地線となるので、2点を結ぶ測地線の中で最短のものが2点の最短距離を示すと考えてよい。その意味で、測地線というのは、2点間の最短距離を測るための曲線の候補の集まりであるともいえる。
ちなみに、2点を北極と南極のような対極の位置に取れば、この2点を結ぶ最短測地線は無数にあることにも注意されたい。
球面では測地線は閉曲線となるが、回転楕円体面上など一般には測地線は閉曲線とならない。
地球あるいは他の天体上で、ある場所とは180°逆に位置する場所。地球においては俗にいう「地球の裏側」である。対蹠点(たいせきてん、たいしょてん)とも言う。数学では3次元のいわゆる球以外の、抽象的な球面に対しても対蹠点という表現を使う。なお、対称点(たいしょうてん)は誤り。
「対蹠」の「蹠」は、「足裏」を意味する語である。従って、「対蹠」とは、「足裏を対する」という意味で、即ち「正反対」を意味する語である。英語のantipodeは、anti(反対)とpode(足)の合成語で、「足を対した所」を意味する。日本で「蹠」を「しょ」と読むのは慣用読みであり、本来の漢音は「せき」である。
対蹠点効果
ある地点から、どんな方角に向かっても対蹠地に着くため、ある地点から発せられた電波(のうち、地上波の一部)は、その対蹠点では、どれかの経路によって通信可能である確率が高く、一般に不安定な短波通信としては比較的には安定である。これを対蹠点効果と呼ぶ(同時に複数の経路からの電波が届くことがあってもマルチパスによるフェージングが発生するため、このことをもって通信品質の向上に寄与すると一概に言えるものではない)。
対蹠点効果は電波以外でもあらゆる波に起こる。地震が起こると、対蹠点周辺では強い揺れが観測される。巨大クレーターの対蹠点には、地震波や衝撃波が集まったことによる「対蹠点地形」が誕生することがある。
吸収などのない理想的な状況では、エネルギー保存則より波の全てのエネルギーが対蹠地に集まり、対蹠地での波の強度は波源での強度と同じになる。そのあと、まるで対蹠地が波源であるかのように、波は対蹠地から再び広がることになる。
思い返せばこの概念を最初に覚えたのは小学生の頃、藤子不二雄「ドラえもん(1969年~)」に登場した以下の平行宇宙論だったのです。「東京から大阪に向かう経路は無数にある。新幹線を使っても使わなくても良いし、飛行機やタクシーを使っても経路としては等価(だからこれからドラえもんが遂行する時間軸を超えての歴史介入はタイムパラドクスを引き起こさない)」

三つ子の魂百までも? とりあえず以下続報…



