【小まとめ】ユークリッド距離と距離空間

①関数y=axの形(傾きaがΔx/Δyで定義される為、関数y=-axとの狭間となるy=0の時点で0除算が発生し計算継続不可能となる)

f:id:ochimusha01:20200109202327g:plain
関数x=ayの形(傾きaがΔy/Δxで定義される為、関数x=-ayとの狭間に該当するx=0で0除算が発生し計算継続不可能となる)
f:id:ochimusha01:20200109203411g:plain

簡単に言うと距離空間（metric space）とは、この様な状況下で書いて直線上の目盛りの一定性を保持する計算方法を模索するジャンルとなります。

距離空間（metric space） - Wikipedia

距離関数と呼ばれる非負実数値関数が与えられている集合のことである。

古代より、平面や空間、地上の 2 点間の離れ具合を表す尺度である距離は測量や科学、数学において重要な役割を果たしてきた。

1906年にモーリス・フレシェは、様々な集合の上で定義された関数の一様連続性の概念を統一的に研究した論文 Fréchet (1906)において、ユークリッド空間から距離の概念を抽出して用い、距離空間の理論を築いた。位相幾何学の成果のうちで距離に関するものを汲み上げ、一般の距離空間の性質として証明しなおして適用することで汎関数の極限を調べたのである。実際、距離を用いて近傍系を定義する事もできるため、位相空間の特殊な例になっている。例えばユークリッド距離とマンハッタン距離であれば、R2 上に同じ近傍系を定めることができるが、異なる近傍系を持つ距離もある。

フェリックス・ハウスドルフは位相空間の重要な性質として距離・近傍系・極限の 3 つを考察し、近傍系を選び位相空間の公理化を行った。そして、極限や連続性などの概念も距離とは無関係に一般化されていった。

こういった一般の位相空間から距離は導かれないので距離空間で論じられる空間は一般の位相空間より狭い範囲のものに限られてしまうが、距離空間は一般の位相空間における定理の意味を掴みやすく、また、位相空間論が応用される集合は距離空間として考えることができる空間が多い為、今なお重要な概念であり続けている。

特に距離が与えられることによって、点同士の関係を実数値として定量的に捉えることができるので、極限や連続性の概念が扱いやすくなる。

同じ集合に対して何種類もの異なる距離関数を考える事も少なくないため、集合X と距離関数dを組にして (X,d) と書いて定義します。

①ユークリッド距離（Euclidean distance）

定義

平面R2 の上の 2 点P1 = (x1, y1), P2 = (x2, y2)について

d1(P1,P2)=sqrt((x1-x2)^2+(y1-y2)^2)

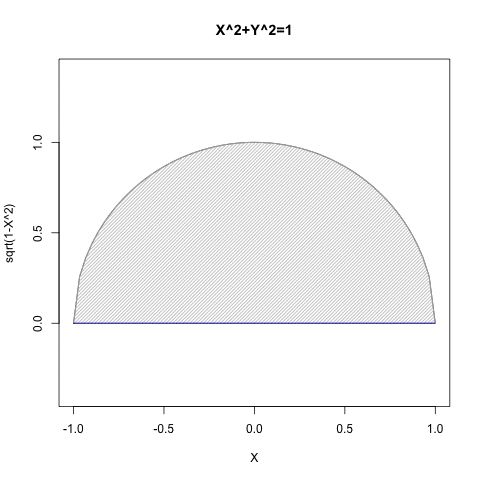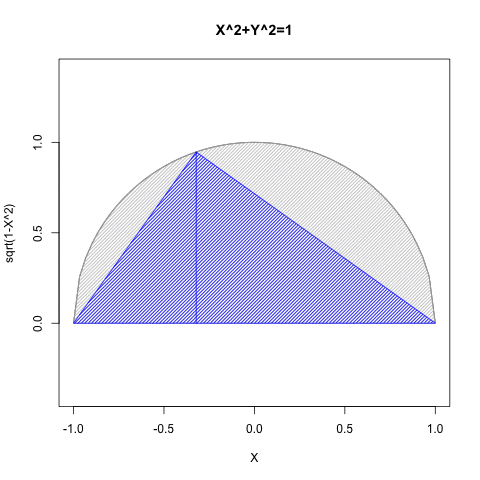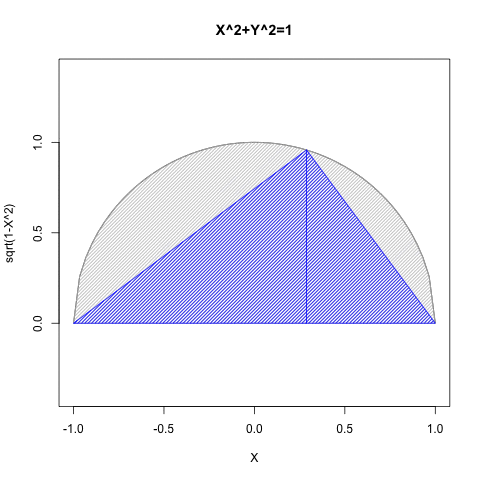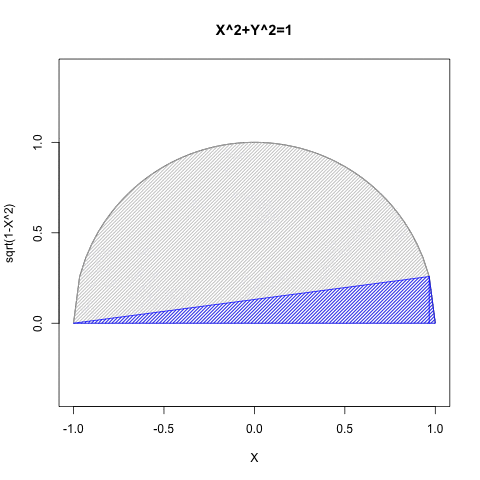
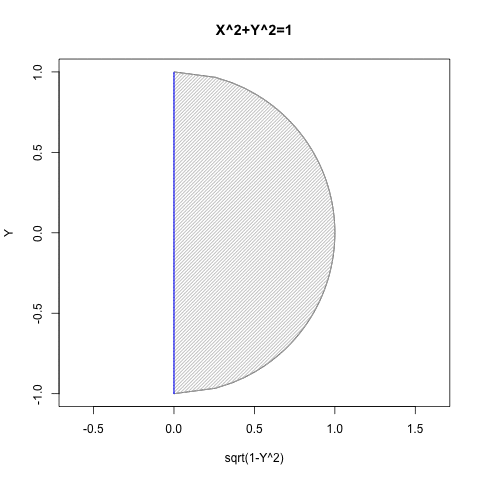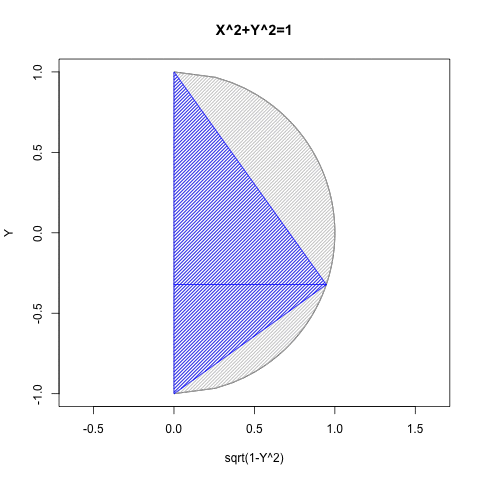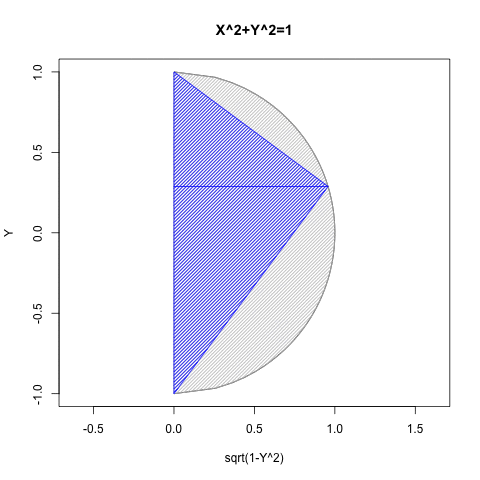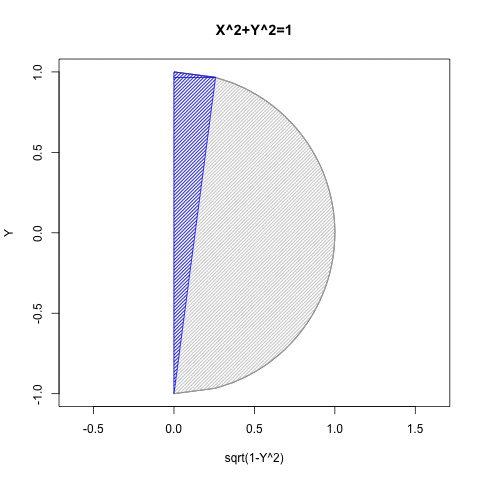
一般に「三平方の定理（Three square theorem）」あるいは「ピタゴラスの定理（Pythagorean theorem）」として知られるX^2+Y^2=Z^2の式、すなわち単位円（Unit Circle、半径1の円弧）上ではx^2+y^2=1、 単位球面（Unit Circle、半径1の円弧）上ではx^2+y^2+z^2=1、となる定理について。しばしばYの値をXで求める関数に変換されたY=sqrt(1-X^2)の形式でも用いられます。

しかしながら三角比(Triangle ratio)すなわち直角三角形（Right triangle）の概念に拘っている限り、X座標もY座標も0以上、すなわち面積が0にならない範囲にしか想像が及ぶ事がなかったのでした。

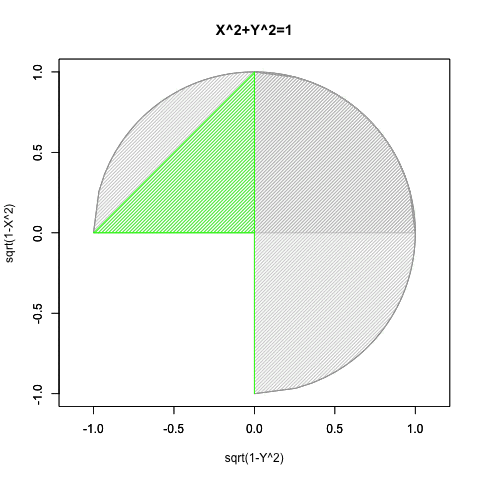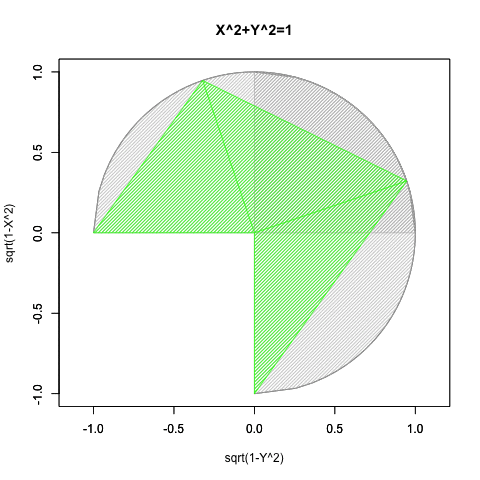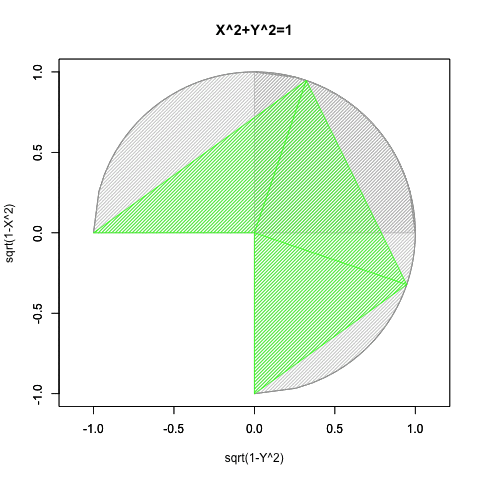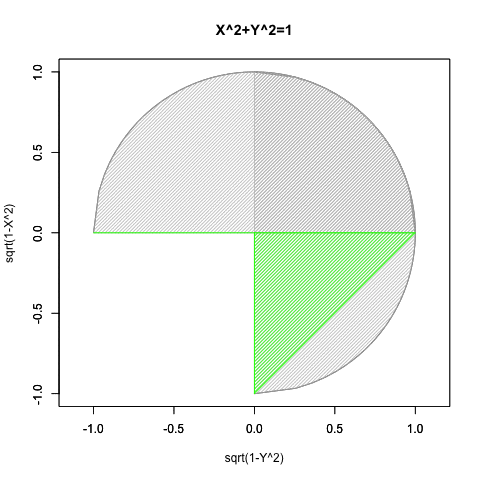
数学史上のある段階まで、この式は関数の制約上「半円しか描けない」「従ってY=sqrt(1-X^2)の式とY=-sqrt(1-X^2)の式のセットなどで運用するもの」と考えられていました。「半円しか描けない」は、正確には以下の状態を指します。

Xの関数としてYを求める場合には（0除算が発生しない）第一象限（X=>0かつY=>0）と第二象限（X=<0かつY=>0）の場合のみ有効。

Yの関数としてXを求める場合には（0除算が発生しない）第一象限（X=>0かつY=>0）と第四象限（Y=<0かつX=>0）の場合み有効。

要するにこのアプローチによっては手が出せないのは、第三象限（X=<0かつY=<0）のみという事になるのです。

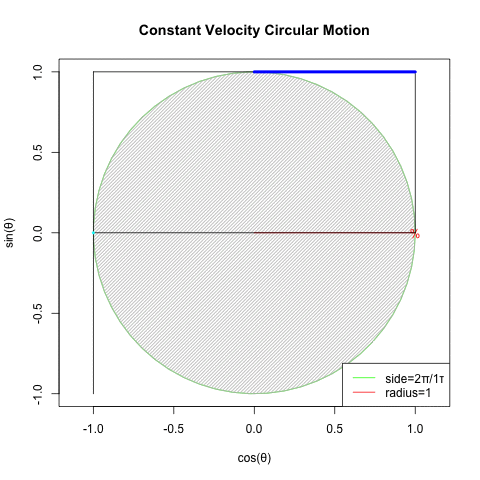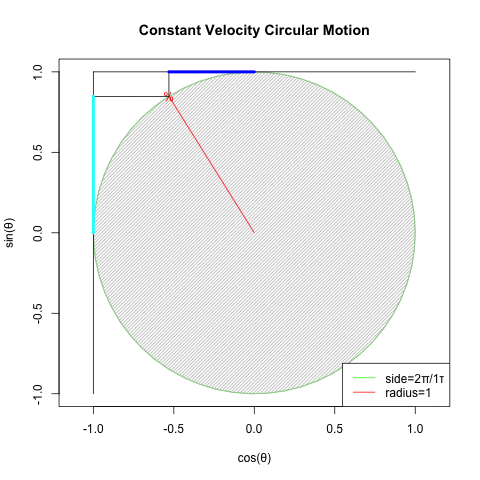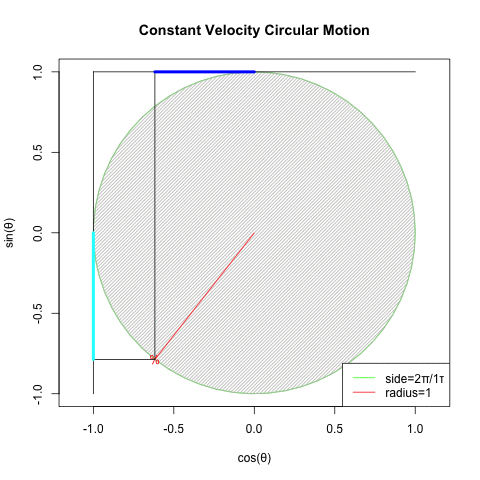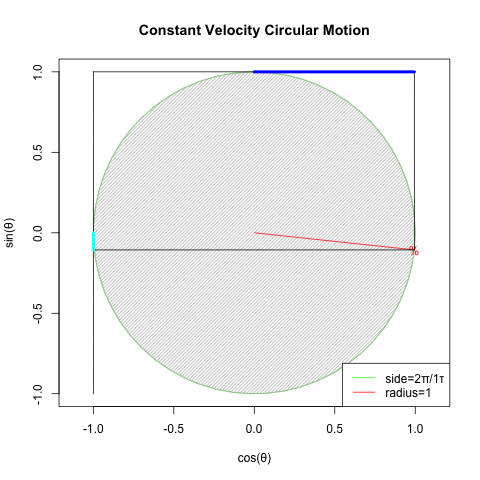
この様に数学方面からの円描画方法の探索は歴史的に行き詰ってしまった訳ですが、ある意味それを打破したのが物理学における等速円運動解析（Constant velocity circular motion）概念の登場だったとも考えられる訳です。

まず「あらゆる運動の原型の一つ」たる等速円運動（Constant Velocity Circular Motion）を想定する。

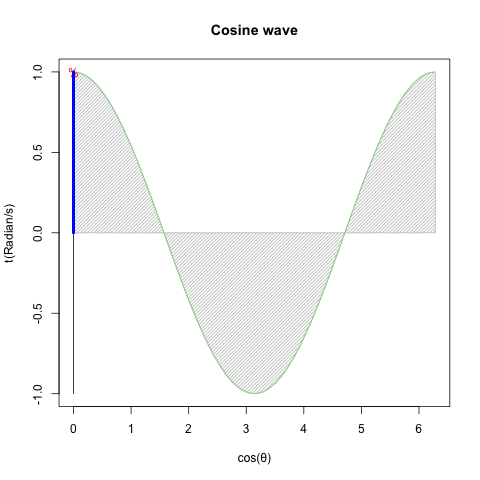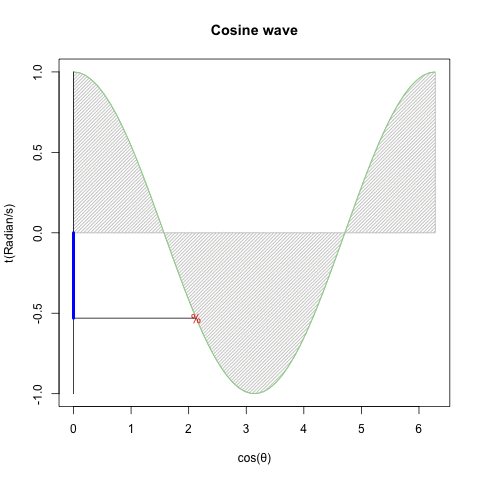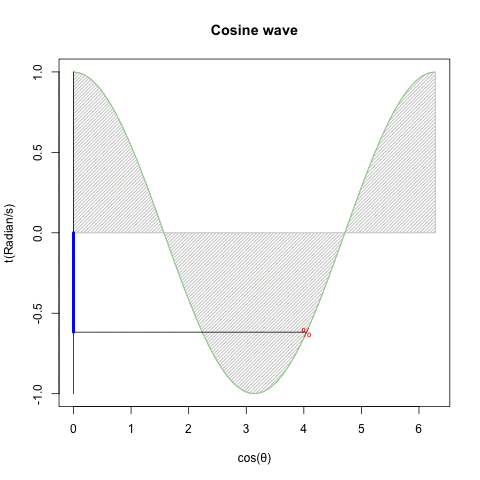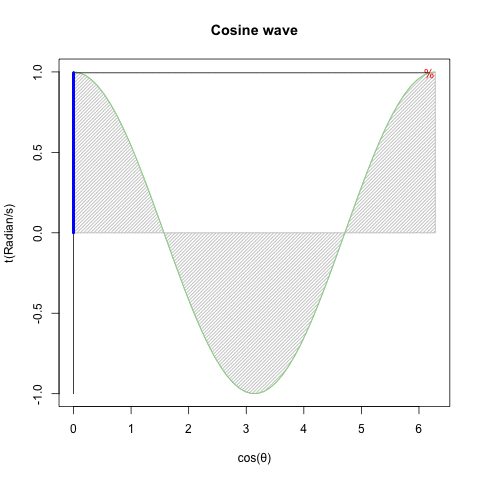
回転運動を互いに直交するX軸側とY軸側から観測すると、同じ波形が互いに位相が90度=π/２ずれた単振動が得られる（Cos波とSin波）逆にこの組み合わせによって回転運動を説明する事も出来る。

ちなみにこのアプローチにおいては（数学における）角度θの概念が角速度（Angular velocity、単位Radian/S）または周波数（frequency、単位Hz）として検出されるので、最終的に構成されるのも「（空間概念としてのみ意識される）単位円（Unit Circle、半径1）」ではなく「（空間として認識されるZ軸と時間経過として意識されるt軸が可換性を有する）単位円筒（Unit Cylinder、半径1、周期1）」となります。

XY軸（円弧）

ZX軸（Cos波）

ZY軸（Sin波）

ここで興味深いのが一般に「三平方の定理（Three square theorem）」あるいは「ピタゴラスの定理（Pythagorean theorem）」として知られるX^2+Y^2=Z^2の式、すなわち単位円（Unit Circle、半径1の円弧）上ではx^2+y^2=1、 単位球面（Unit Circle、半径1の円弧）上ではx^2+y^2+z^2=1、となる定理との関係。

コンピューター言語は無限大Infの辺数と無限小-Infの辺長で構成される円そのもの(circle itself)を直接は扱えないので、これを適切な精度が得られる正多角形として扱うしかない（このサイトでは主に正60角形を採用）。

その状態で上掲式を適用するとヒストグラムとしてNoD(Number of Divide=分割数)に対応する半径長の線分集合が得られるのである。

class frequency

1 0 ～ 1 60

ユークリッド距離自体についての言及は以上？